iso tank 2019年 08月

以前、さくらのレンタルサーバの仕様とblosxomの仕様の兼ね合いで若干問題が生じることについて触れた。

が、実は2017年3月に仕様変更があり、MultiViewsオプションが使用できるようになっていた。

以前書いたとおり、blosxomのカテゴリとして使用するディレクトリと同じ名前のファイルを設置すると、カテゴリに遷移した時にファイルの方の中身がぶちまけられてしまう、という問題があったが、

Options -MultiViews

と.htaccessに記述するだけで、ファイル名とディレクトリ名がカブっても問題なく動作するようになる。

以前から直っていたが、記事をそのまま放置してしまっていた。

ただし、環境変数を追加できない問題だけは解決していない。が、これは仕方ないと思うし、むしろコードの方がある程度自由に弄られることを許容してるんじゃないかな？　と考えてたりもする。自分のスキル不足もある。

先日貼ったクイックソートのコードにもちょっとだけ使ってたが、XOR（排他的論理和）を利用して色々と面白いことができる。

有名なのはXOR交換アルゴリズムだが、これは二つの変数に格納されている値を交換するとき、一時変数を介すことなくXORだけで二つの変数の値を交換してしまえるという手法。VBAで記述すると以下のようになる。

A = A Xor B
B = A Xor B 'Aの値が代入される
A = A Xor B 'Bの値が代入される

なぜこうなるのか？　2行目を数式にすると、

(A Xor B) Xor B = A

である。XORは括弧の有無や括弧の位置を変えても計算結果は変わらない（結合法則）。なので、

B Xor B Xor A = A

でも同じである。XORは排他的論理和（2値がどちらも真または偽の場合は偽、それ以外は真）であるので、同じ値をXORすると0になる。よって、

(B Xor B) Xor A = A
0 Xor A = A
A = A

である（Aと0をXORした場合はそのままAが返る）。つまり、 A XOR B の結果（仮にA'とする）をもう一度BとXORすることでAを求めることができ、同様にA'をAとXORすればBが求められる。XORは非常に面白い性質を持っている。

ちなみに、XOR交換は3値以上でも成り立つ。要は複数の値を全てXORした結果に対し、ある一値以外のすべての値をXORしてやれば、その一値が求められる。

A = A Xor B Xor C Xor D Xor E Xor F
B = A Xor B Xor C Xor D Xor E Xor F 'Aの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor B Xor C Xor D Xor E Xor F と等価）
C = A Xor B Xor C Xor D Xor E Xor F 'Bの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor A Xor C Xor D Xor E Xor F と等価）
D = A Xor B Xor C Xor D Xor E Xor F 'Cの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor A Xor B Xor D Xor E Xor F と等価）
E = A Xor B Xor C Xor D Xor E Xor F 'Dの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor A Xor B Xor C Xor E Xor F と等価）
F = A Xor B Xor C Xor D Xor E Xor F 'Eの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor A Xor B Xor C Xor D Xor F と等価）
A = A Xor B Xor C Xor D Xor E Xor F 'Fの値が代入される（A Xor B Xor C Xor D Xor E Xor F Xor A Xor B Xor C Xor D Xor E と等価）

で。ふと、XOR交換以外にも色々と応用が利くんじゃないか？　と思った。具体的には条件分岐の代用とか。探したところ、研究員の津田氏のブログ「津田の開発な日記」にて条件分岐を使わずにmax/min関数を実現する方法というものが公開されていた。以下引用。

int max(int a, int b) {
    return a ^ ((a ^ b) & -(a < b));
}

これをVBAで書くとこうなる。

Public Function max(ByRef a As Long, ByRef b As Long) As Long
    Let max = a Xor ((a Xor b) And (a < b))
End Function

このC言語の例では比較演算の真値が1となるため正負反転を行っているが、VBでは真値が-1となる（偽はいずれも0）ので、正負の反転は必要ない。要は、a < b が成立するなら a Xor ((a Xor b) And -1) = b、成立しなければ a Xor ((a Xor b) And 0) = a となり、ちゃんとmax関数としての機能を果たしている。ちなみに-1は全てのビット列が1、つまり0が裏返った値なので、A And -1 = Aとなる。

なおmin関数は、このmax関数のコードの不等号を反転するか、あるいは最初のaをbにするだけでいい。

Public Function min(ByRef a As Long, ByRef b As Long) As Long
    Let min = b Xor ((a Xor b) And (a < b))
End Function

ちなみに先のブログによれば、不等号の部分は条件分岐になっていない（アセンブラコード上では分岐命令を使用していない）、とのこと。ただしあくまでもC言語での話なので、VBでどうなってるかは不明。分岐命令を使っているとしたら動作は遅くなるかもしれない。

まぁ、最初の予想に反してXORだけで条件分岐の代わりをすることは難しいが、他の演算と組み合わせて条件分岐の代わりになる、ということは分かった。

で、これを応用すれば3値の中央値(median)を求めることも可能なんじゃないか？　と思い立った。要は偶数回出現した値は消えて奇数回出現した値は残るんだから、以下の計算で中央値が求められるはずだ。

A Xor B Xor C Xor max(A, B, C) Xor min(A, B, C) = median

A・B・C・最大値・最小値の5つをXORすることで、最大値と最小値はそれぞれ2回（偶数回）、中央値は1回（奇数回）だけ演算することになり、中央値のみが残る。早速やってみる。

Public Function med(ByRef A As Long, ByRef B As Long, ByRef C As Long) As Long
    Dim tmpMax&, tmpMin&
    Let tmpMax = A Xor ((A Xor B) And (A < B))
    Let tmpMin = A Xor ((A Xor B) And (A > B))
    Let med = A Xor B Xor C Xor _
              (C Xor ((C Xor tmpMax) And (C < tmpMax))) Xor _
              (C Xor ((C Xor tmpMin) And (C > tmpMin)))
End Function

できた。

これでもちゃんと動くが、冗長すぎる。もうちょっとスマートにしたい。どうすればいいか考えていたところ、C を2回続けてXORしている部分の外側の方のXor C は、演算の優先順位を下げても演算結果に影響しないことに気付いた（結合法則）。

    Let med = A Xor B Xor C Xor _
              C Xor ((C Xor tmpMax) And (C < tmpMax)) Xor _
              C Xor ((C Xor tmpMin) And (C > tmpMin))

上記のように左端の方のXor C を括弧の外に出しても演算結果は変わらない。すると、同じ優先順位の層で C が何度もXORされていることになる。XORは可換（XOR以外の演算と結合しない箇所であれば位置を交換しても結果が同じ）なので、

    Let med = A Xor B Xor C Xor C Xor C Xor _
              ((C Xor tmpMax) And (C < tmpMax)) Xor _
              ((C Xor tmpMin) And (C > tmpMin))

としても演算結果は同じである。ところで先に述べたとおり、同じ値を奇数回XORすると元の値に戻る。なので Xor C を3回も繰り返す必要はない。1回で十分である。

    Let med = A Xor B Xor C Xor _
              ((C Xor tmpMax) And (C < tmpMax)) Xor _
              ((C Xor tmpMin) And (C > tmpMin))

A・B・C・3値の最大値・3値の最小値をXORするはずだったのに、2行目と3行目の内容が変わってしまった。それでも演算結果は変わらない。どういうことか。

2行目は「C < max(A, B) の場合は (C Xor max(A, B)) を XORする」、3行目は「C > min(A, B) の場合は (C Xor min(A, B)) を XORする」、ということだ。

A < B < C と仮定してみると、2行目は C < B が偽となり0、3行目は C > A が真となり1行目の結果に A Xor C をXORし、最終的に B が返る。

逆に A > B > C と仮定すると、2行目は C < A が真で A Xor C、3行目は C > B が偽となり0。結果はやはりB。

では B < A < C の場合は？　A Xor B Xor C Xor 0 Xor B Xor C で結果はA。B < C < A だと A Xor B Xor C Xor A Xor C Xor B Xor C で結果はC。

この時、なにか閃いた。これはたぶんなんかこういうことだ！　と走り書きしたメモが以下。

'たぶんなんかこういうやつ。
If A < B Then
    'A Xor B
    If B < C Then
        'B Xor C
    ElseIf C < A Then
        'C Xor A
    End If
ElseIf B < C Then
    'B Xor C
    If C < A Then
        'C Xor A
    End If
ElseIf C < A Then
    'C Xor A
End If

'以下に置き換えられるはず。
If A < B Then
    'A Xor B
End If
If B < C Then
    'B Xor C
End If
If C < A Then
    'C Xor A
End If

たぶんなんかこういうやつ。で、できたのが以下のコード。

Public Function med3(ByRef A As Long, ByRef B As Long, ByRef C As Long) As Long
    Let med3 = A Xor B Xor C Xor ((A Xor B) And (A < B)) Xor ((B Xor C) And (B < C)) Xor ((C Xor A) And (C < A))
End Function

何をやっているかというと、A XOR B XOR C の演算結果に対し、A < B のときは A と B、B < C のときは B と C、C < A のときは C と A をそれぞれXORしている。

こうすると3値の中央値を求めるために最大値・最小値を求める必要がないため、計算量も減ったし一時変数も不要になった。ダラダラした条件分岐を使う必要もない。キモチイイ！

ただし、

'Ifを使わずに中央値を求める関数
Public Function med3(ByRef A As Long, ByRef B As Long, ByRef C As Long) As Long
    Let med3 = A Xor B Xor C Xor ((A Xor B) And (A < B)) Xor ((B Xor C) And (B < C)) Xor ((C Xor A) And (C < A))
End Function

'Ifを使って中央値を求める関数
Public Function medIF(ByRef A As Long, ByRef B As Long, ByRef C As Long) As Long
    If A < C Then
        If B < A Then
            Let medIF = A
        ElseIf B < C Then
            Let medIF = B
        Else
            Let medIF = C
        End If
    ElseIf A < B Then
        Let medIF = A
    ElseIf C < B Then
        Let medIF = B
    Else
        Let medIF = C
    End If
End Function

'乱数発生器
Private Function RandomLong(ByRef minVal As Long, ByRef maxVal As Long, Optional ByRef doRandomize As Boolean = True) As Long
    If doRandomize Then
        Randomize
    End If
    Let RandomLong = Int(Rnd * (maxVal - minVal + 1)) + minVal
End Function

'速度検証
Sub SpeedTestMed()
    Dim A As Long
    Dim B As Long
    Dim C As Long
    Dim M As Long
    Dim i As Long
    Dim loopCnt As Long
    Dim pTime As Single
    Let A = RandomLong(1, 200000000)
    Let B = RandomLong(1, 200000000)
    Let C = RandomLong(1, 200000000)
    Let loopCnt = 5000000
    Let pTime = Timer
    For i = 1 To loopCnt
        Let M = medIF(A, B, C)
    Next i
    Debug.Print "medIF:" & Timer - pTime    'medIF:0.4296875
    Let pTime = Timer
    For i = 1 To loopCnt
        Let M = med3(A, B, C)
    Next i
    Debug.Print "med3: " & Timer - pTime    'med3: 0.4453125
End Sub

少なくとも自分の環境のVBAでは、普通にIfで条件分岐した方が速い。

2019/08/26　追記

Public Function med3(ByRef A As Long, ByRef B As Long, ByRef C As Long) As Long
    Let med3 = A Xor B Xor C Xor ((A < B) And (A Xor B)) Xor ((B < C) And (B Xor C)) Xor ((C < A) And (C Xor A))
End Function

以前書いたコードとAndの前後が入れ替わっているが、結果には影響しない。左から読んで「『A < B』なら『A Xor B』」と読めるので、自分はこの順番の方が好き。

なぜこの数式で中央値が求められるのか、少し掘り下げてみる。XORについてはベン図を使うとわかりやすい。A < B < C と仮定し数式を左から順に読み解くと、

A

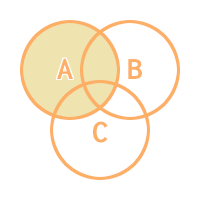
Xor B

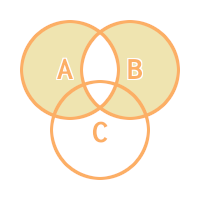
Xor C

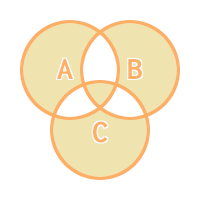
Xor ((A < B) And (A Xor B))

の(A < B)は今回の仮定では真(-1)であり、

Xor ((-1) And (A Xor B))
= Xor (A Xor B)
= Xor A Xor B

となるので、Xor A と Xor B に分解してそれぞれ評価してみる。

Xor A

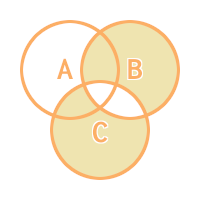
Xor B

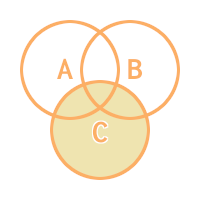
次。

Xor ((B < C) And (B Xor C))

これも(B < C)は真(-1)なので、上と同様にXor B と Xor C に分解。

Xor B

Xor C

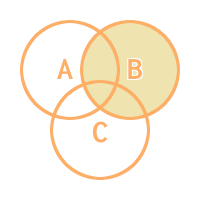
次。

((C < A) And (C Xor A))

の(C < A)は偽(0)なので、

Xor ((0) And (C Xor A))
= Xor (0)
= Xor 0

0をXORしても値は変わらないので、

がそのまま結果となる。

他のパターンでも同様に求めることができる。

また、3値のうち2値が同値だった場合はその2値の方が返るようになっている。

3値とも同値だった場合は、もちろんその値が中央値となる。

洋々亭にて、様々なVBAコードが公開されている。

この中に含まれている、丸付き数字（「○２」など）を丸囲み数字（「②」など）に変換する関数を、⓪～㊿まで対応できるように改造した。

ちなみになんでこんな関数が必要かというと、一部の法令（児童福祉法など）は、項番号の代わりに丸数字を使用していることがあるが、丸数字は機種依存文字（環境依存文字）なので正しく表示されないコンピュータが存在する恐れがあり、e-Govでは「○２」としている。これを本来意図するところの丸数字に置き換えるため。

現在ではほとんどの機種（環境）で丸数字が表示できるようになっており、これを一括変換したいという要望があったので、洋々亭のコードを拝借し、かつ範囲を広げた。

'---------------------------------------------------------------------------------------------------
' 丸付き数字置換関数
' ◆機能の説明
'   ・「○３」形式の表記を「③」に変換する
'   ・一部文字列はUnicode文字に変換する
'   ・一定数を超える数字の場合は丸囲み数字が使用できないため、角かっこで囲む（○５１→[51]）
'   ※項番号を上記の方法で表記している法令があるための対処（児童福祉法等）。
' オリジナル：洋々亭 2006
'---------------------------------------------------------------------------------------------------
Private Function ToCircledNum(ByRef srcStr As String) As String
    
    Dim srcLen As Long      '引数の文字列長（○を含む）
    Dim tmpAsc As String    '引数から○を除去し半角英数に変換した文字列
    Dim chrNum As Long      '変換後の数字
    Dim i As Long           'イテレータ
    
    'まず全角数字を半角数字に置き換え、次に半角数字を丸数字に置き換える。
    Let srcLen = Len(srcStr)
    If srcLen < 2 Then
        Exit Function
    End If
    Let tmpAsc = String$(srcLen - 1, vbNullChar)
    For i = 2 To srcLen
        Mid(tmpAsc, i - 1, 1) = Mid$("0123456789", CLng(InStr("０１２３４５６７８９", Mid$(srcStr, i, 1))), 1)
    Next i
    Let chrNum = CLng(tmpAsc)
    Select Case chrNum
    Case Is < 0                                 '0未満は非対応([]で括る)
        Let ToCircledNum = "[" & tmpAsc & "]"
    Case 0                                      '丸0  = U+24EA( 9450) chrNum=0のためそのまま
        Let ToCircledNum = ChrW(9450)
    Case Is < 21                                '1～20は普通に丸囲み数字が使用できる
        Let ToCircledNum = Mid$("①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮⑯⑰⑱⑲⑳", chrNum, 1)
    Case Is < 36                                '丸21 = U+3251(12881) 21から始まるため 12881 - 21 = 12860
        Let ToCircledNum = ChrW(12860 + chrNum)
    Case Is < 51                                '丸36 = U+32B1(12977) 36から始まるため 12977 - 36 = 12941
        Let ToCircledNum = ChrW(12941 + chrNum)
    Case Else                                   '51以上も非対応([]で括る)
        Let ToCircledNum = "[" & tmpAsc & "]"
    End Select
End Function

「引数には丸記号＋全角英数字の組み合わせの文字列しか来ない」という前提で作ってる関数なので、呼び出し前に正規表現やLikeマッチングでのふるい落としが必要。簡単な判定は19行目でやってるけど（引数が1文字以下なら何も返さず終了）。

やってることは洋々亭のmarumoji関数と一緒。まず全角英数字を半角英数字に置き換え（22～25行目）、整数型に変換（26行目）。あとはSelect Case文で0未満と50超は対応する丸数字がないため[]で括る、⓪と㉑～㊿はChrW関数で文字コードから文字を取得。①～⑳は文字を並べてMid関数で対応する数字の位置に該当する文字を取得。

①～⑳もChr関数を使えば取得できるが、文字を並べてMid関数で取得した方がちょっとだけ早い。

Public Sub SpeedTest()
    Dim testNums(2000000) As Long
    Dim dummyStr As String
    Dim procTime As Single
    Dim i As Long
    For i = LBound(testNums) To UBound(testNums)
        Let testNums(i) = RandomLong(1, 20)
    Next i
    Let procTime = Timer
    For i = LBound(testNums) To UBound(testNums)
        Let dummyStr = Mid$("①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮⑯⑰⑱⑲⑳", testNums(i), 1)
    Next i
    Debug.Print "Test1: " & Timer - procTime        'Test1: 0.140625
    Let procTime = Timer
    For i = LBound(testNums) To UBound(testNums)
        Let dummyStr = Chr(34623 + testNums(i))
    Next i
    Debug.Print "Test2: " & Timer - procTime        'Test2: 0.171875
End Sub

Private Function RandomLong(ByRef minVal As Long, ByRef maxVal As Long, Optional ByRef doRandomize As Boolean = True) As Long
    If doRandomize Then
        Randomize
    End If
    Let RandomLong = Int(Rnd * (maxVal - minVal + 1)) + minVal
End Function

⓪～㊿を全部並べてMid関数で取得した方が分かりやすいしできるならそうしたいんだけど、VBAは内部的にUnicode文字を使用しているものの、VBEはUnicode文字をサポートしていない。

ChrW関数などを使用してUnicode文字をサポートしている出力先（例えばWord文書など）に出力すること自体は可能なので、こういった書き方になった。もっとスマートな方法はないだろうか。

別になんてこたないんだけどね。

highlightjs.orgというサイトで公開されているライブラリを使用すれば、ブログ記事とかにプログラムのコードを貼り付けると自動的にシンタックスハイライトをしてくれるらしい。

blosxomのプラグインとしてコードをシンタックスハイライトする奴を作ろうかなー、とか思ってたけど既にあったわ。という話。

というわけで、ちょっと実験。

Option Explicit

'---------------------------------------------------------------------------------------------------
' クイックソート関数（SourceArray   <配列>）
'   説明： 渡された配列の要素をクイックソート（非安定ソート）で昇順に並び替える。
'---------------------------------------------------------------------------------------------------
Public Function QuickSort(ByVal SourceArray As Variant) As Variant
    
    Dim valLEnd As Variant      '左端の値
    Dim valREnd As Variant      '右端の値
    Dim valMed As Variant       '中央値
    Dim valSwap As Variant      'バッファ（値交換用）
    Dim posLEnd As Long         '左端の位置
    Dim posREnd As Long         '右端の位置
    Dim posLEnds() As Long      '左端の位置を記憶するスタック（配列）
    Dim posREnds() As Long      '右端の位置を記憶するスタック（配列）
    Dim topStack As Long        'スタック(配列)の最大添字 ※スタック確保用
    Dim bottomStack As Long     'スタック(配列)の最小添字 ※Option Base 1 への対策用（念の為）
    Dim ptrStack As Long        'スタック（配列）のポインタ
    Dim ptrLtoR As Long         '左端から右に向かって探索するポインタ（Lポインタと呼称）
    Dim ptrRtoL As Long         '右端から左に向かって探索するポインタ（Rポインタと呼称）
    
    '初期処理
    If Not IsArray(SourceArray) Then
        Exit Function
    End If
    Let posLEnd = LBound(SourceArray)   '引数の左端の位置
    Let posREnd = UBound(SourceArray)   '引数の右端の位置
    Let bottomStack = LBound(Array())   'スタックの最小添字
    Let topStack = Int(Log(posREnd - posLEnd + 1) / Log(2)) + bottomStack  'スタックサイズはLog2(n)個で足りる
    ReDim posLEnds(topStack)            'スタック確保
    ReDim posREnds(topStack)
    Let ptrStack = bottomStack          '全体範囲をスタックにPUSH
    Let posLEnds(ptrStack) = posLEnd
    Let posREnds(ptrStack) = posREnd
    
    'メイン処理
    Do Until ptrStack < bottomStack     'すべてのスタックが処理されるまで繰り返す
        
        '探索範囲POP・値取得
        Let posLEnd = posLEnds(ptrStack)    'スタックから両端の位置を取り出す
        Let posREnd = posREnds(ptrStack)
        Let ptrLtoR = posLEnd               '両端の位置をLポインタ・Rポインタにそれぞれセット
        Let ptrRtoL = posREnd
        Let valLEnd = SourceArray(ptrLtoR)  '両端の値と中間位置の値を取得
        Let valREnd = SourceArray(ptrRtoL)
        Let valMed = SourceArray(ptrLtoR + Int((ptrRtoL - ptrLtoR) / 2))
        
        '中央値導出（左端の値・右端の値・中間位置の値、の3値から中央値を求める）
        If valLEnd > valMed Then
            If valREnd > valLEnd Then
                Let valMed = valLEnd
            ElseIf valREnd > valMed Then
                Let valMed = valREnd
            End If
        ElseIf valLEnd > valREnd Then
            Let valMed = valLEnd
        ElseIf valMed > valREnd Then
            Let valMed = valREnd
        End If
        
        '探索・値交換
        Do Until ptrLtoR > ptrRtoL          'LポインタとRポインタの位置が逆転するまで繰り返す
            Do Until SourceArray(ptrLtoR) >= valMed
                Let ptrLtoR = ptrLtoR + 1   '左から右へ、中央値以上の値の位置を探索する
            Loop
            Do Until SourceArray(ptrRtoL) <= valMed
                Let ptrRtoL = ptrRtoL - 1   '右から左へ、中央値以下の値の位置を探索する
            Loop
            If ptrLtoR > ptrRtoL Then
                Exit Do                     'LポインタとRポインタの位置が逆転したら探索・値交換を終了する
            End If
            If ptrLtoR < ptrRtoL Then       'Lポインタ＜Rポインタ であれば、左の値と右の値を交換する
                Let valSwap = SourceArray(ptrLtoR)  '（左の値は中央値以上、右の値は中央値以下になっている）
                Let SourceArray(ptrLtoR) = SourceArray(ptrRtoL)
                Let SourceArray(ptrRtoL) = valSwap
            End If
            Let ptrLtoR = ptrLtoR + 1       'Lポインタ≦Rポインタ であれば、範囲を1つずつ狭める
            Let ptrRtoL = ptrRtoL - 1
        Loop
        
        '探索範囲の分割・交換（左範囲［左端～交差したRポインタ］ 右範囲［交差したLポインタ～右端］）
        If ptrRtoL - posLEnd < posREnd - ptrLtoR Then   '※ポインタの間に要素がある場合、その要素の位置は確定
            Let ptrLtoR = ptrLtoR Xor posLEnd   '左範囲と右範囲で、範囲の広い方を先にスタックするように調整
            Let posLEnd = ptrLtoR Xor posLEnd   '何もなければ左範囲→右範囲の順でスタックするようになっている
            Let ptrLtoR = ptrLtoR Xor posLEnd   '右範囲の方が左範囲より広ければ、左右の端の位置とポインタを交換
            Let ptrRtoL = ptrRtoL Xor posREnd   '左端←→Lポインタ、Rポインタ←→右端
            Let posREnd = ptrRtoL Xor posREnd   'スタックのサイズをLog2(n)以下に抑えられるようになる
            Let ptrRtoL = ptrRtoL Xor posREnd
        End If
        
        '探索範囲（広い方）PUSH
        If posLEnd < ptrRtoL Then               '範囲内の要素が2以上あればスタックにPUSHする
            Let posLEnds(ptrStack) = posLEnd    '（1つしかない場合はその要素の位置が確定したためPUSHしない）
            Let posREnds(ptrStack) = ptrRtoL    '現在処理中のスタックは上書きされる（実質的にPOPと同じ動作）
            Let ptrStack = ptrStack + 1         'スタックポインタに1加算＝次の空きスタックへ移動
        End If
        
        '探索範囲（狭い方）PUSH
        If ptrLtoR < posREnd Then               '上記と同じ処理
            Let posLEnds(ptrStack) = ptrLtoR
            Let posREnds(ptrStack) = posREnd
            Let ptrStack = ptrStack + 1
        End If
        
        '最上位スタックへポインタ移動
        Let ptrStack = ptrStack - 1
    Loop
    Let QuickSort = SourceArray
End Function

コードは前に何かで使ったクイックソート。さて、どうかな？